Langsung ke konten utama

4 - INTRODUCTION TO TREE, BINARY TREE AND EXPRESSION TREE - 2101714345 - Vallentina Chisty

Vallentina Christy / 2101714345 / CA01


INTRODUCTION TO TREE, BINARY TREE AND EXPRESSION TREE

Related image

TREE AND BINARY TREE


Tree Concept

Tree merupakan sebuah koleksi atas satu atau lebih nodes.
Image result for tree data structure
Node yang berada paling atas disebut root.
Sebuah garis yang menghubungkan parent dengan child disebut edge.
Nodes yang tidak memiliki child disebut leaf.
Nodes yang memiliki parent yang sama disebut sibling.
Degree dari node merupakan total sub tree dari node.
Height / Depth merupakan maximum degree dari nodes pada tree.
Jika terdapat garis yang menghubungkan p kepada q, maka p disebut ancestor dari q, dan q disebut descendant dari p.

Binary Tree Concept

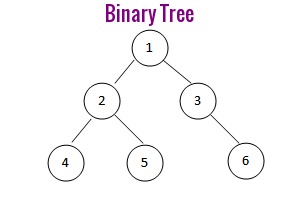
Image result for binary tree data structure
Binary tree merupakan percabangan tree data structure dimana setiap node memiliki paling banyak dua children yaitu child kiri dan child kanan.

Type of Binary Tree

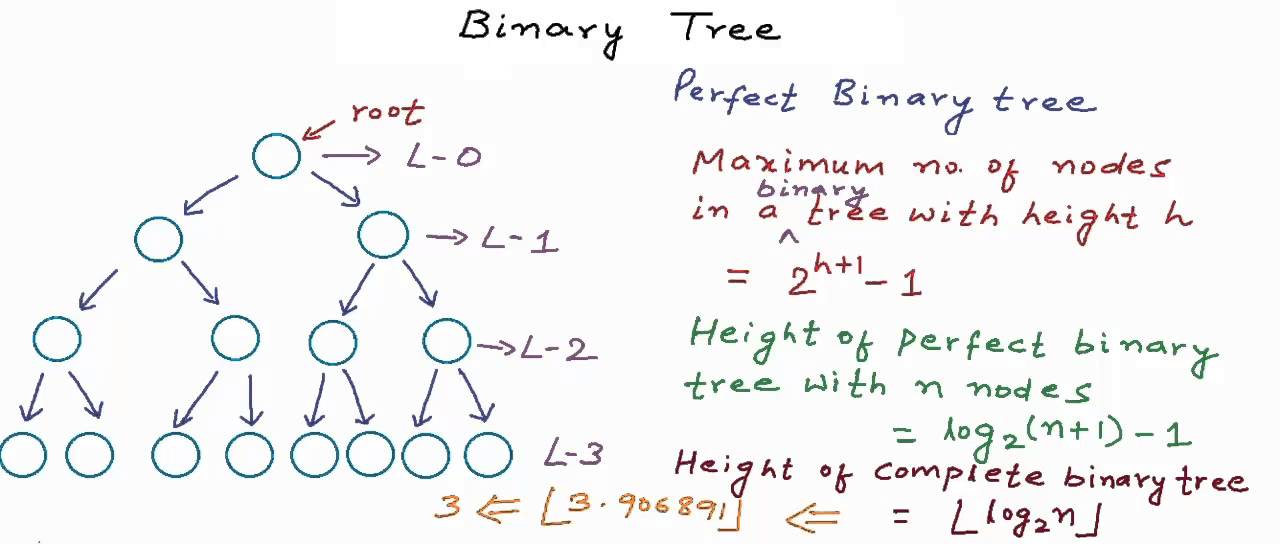
PERFECT Binary Tree merupakan binary tree dimana di setiap level memiliki depth / kedalaman / lebar yang sama.
Image result for perfect binary tree

COMPLETE Binary Tree merupakan binary tree dimana setiap level terisi penuh (kecuali mungkin yang terakhir) dan semua nodes akan mengarah ke bagian kiri tree. Perfect binary tree juga merupakan complete binary tree.
Image result for COMPLETE binary tree

SKEWED Binary Tree merupakan binary tree dimana setiap node memiliki paling banyak satu child.
Image result for skewed binary tree

BALANCED Binary Tree merupakan binary tree dimana setiap leaf memiliki jarak yang sama terhadap root.
Image result for balanced tree

Property of Binary Tree

Maximum number dari nodes pada level k dari sebuah binary tree dapat dituliskan sebagai 2 pangkat k.
Related image

Related image

Representation of Binary Tree

- Implementation using array
Image result for binary tree implementation using array

- Implementation using linked list
Image result for binary tree using linked list

Expression Tree Concept

Kita dapat membuat sebuah expression tree dari prefix ataupun postfix dengan proses rekursif.

Konsep dari expression tree:
  • Prefix : Print L R
    Contoh :     *+ab/-cde
  • Postfix : L R Print
    Contoh :     ab+cd-e/*
  • Infix : L Print R
    Contoh :     (a+b)*((c-d)/e)

Prefix Traversal

Di prefix, kita harus print / proses sebelum child tersebut diproses.

Postfix Traversal

Di postfix, kita harus print / proses setelah child tersebut telah diproses.








Komentar

Posting Komentar

Postingan populer dari blog ini

3 - LINKED LIST IMPLEMENTATION 2 - 2101714345 - Vallentina Christy

Vallentina Christy / 2101714345 / CA01 LINKED LIST IMPLEMENTATION 2 STACK Stack merupakan salah satu tipe data structure yang cukup penting dimana stack itu sendiri menyimpan elemen-elemen seraca berurutan. Stack juga merupakan linear data structure yang dapat diimplementasikan dengan menggunakan array maupun linked list. Elemen dalam stack ditambah maupun dikurangi di hanya di satu edge, edge ini disebut top. Stack berlaku First In Last Out (FILO) atau Last In First Out (LIFO). Stack memiliki 2 variabel, TOP (digunakan untuk menyimpan alamat dari elemen paling atas) dan MAX (digunakan untuk menyimpan maximum number dari elemen yang dapat ditampung oleh stack). Di dalam linked stack, setiap node memiliki dua bagian, yang pertama menyimpan data dan yang kedua menyimpan alamat dari node berikutnya. Pointer START pada linked list digunakan sebagai TOP. Semua insertion dan deletion diselesaikan di node oleh TOP. Jika TOP = NULL maka itu berarti bahwa stac
Posting Komentar
Baca selengkapnya

2 - LINKED LIST IMPLEMENTATION 1 - 2101714345 - Vallentina Christy

Vallentina Christy / 2101714345 / CA01 LINKED LIST IMPLEMENTATION 1 LINKED LIST Linked list merupakan koleksi linear dari data, yang disebut node, dimana setiap node akan menunjuk pada node lain melalui sebuah pointer. Linked list juga dapat didefinisikan sebagai kumpulan node yang mempresetasikan sebuah sequence. SINGLE LINKED LIST Single linked list merupakan linked list yang menggunakan sebuah pointer untuk menyimpan banyak data. Pointer hanya dapat bergerak ke satu arah saja. Single Linked List : Insert Front Penambahan data di depan membutuhkan penambahan node baru yang akan dikaitkan di node paling depan, tetapi pada saat pertama kali, saat data masih kosong, penambahan data dilakukan pada head nya. Untuk menghubungkan node yang terakhir dengan node yang terdepan dibutuhkan pointer baru. Back Penambahan data di belakang tentu saja dilakukan di belakang. Pada saat pertama kali, data langsung ditunjuk pada head nya. Kita me
Posting Komentar
Baca selengkapnya

5 - TREE AND BINARY TREE - 2101714345 - Vallentina Christy

Vallentina Christy / 2101714345 / CA01 TREE AND BINARY TREE BINARY TREE CONCEPT Gambar diatas merupakan contoh binary tree dengan 8 nodes, dimana node yang berisi nomer 1 merupakan root dan node yang berisi nomer 6, 7, 8, dan 3 merupakan leaf atau leaves. TYPE OF BINARY TREE PERFECT Binary Tree  merupakan binary tree dimana di setiap level memiliki depth / kedalaman / lebar yang sama. COMPLETE Binary Tree  merupakan binary tree dimana setiap level terisi penuh (kecuali mungkin yang terakhir) dan semua nodes akan mengarah ke bagian kiri tree. Perfect binary tree juga merupakan complete binary tree. SKEWED   Binary Tree  merupakan binary tree dimana setiap node memiliki paling banyak satu child. BALANCED Binary Tree  merupakan binary tree dimana setiap leaf memiliki jarak yang sama terhadap root. PROPERTY OF BINARY TREE Maximum number dari nodes pada level  k  dari sebuah binary tree dapat dituliskan sebagai 2 pangkat  k .
Posting Komentar
Baca selengkapnya